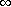HOMEWORK helpline - Open 24 hours

First Previous

Page

Next Last

Frequent Posters

Sonia

@Miggi

Inactive

Posted: 15 years ago

#231

Consider the function below. (Round the answers to two decimal places. If you need to use -

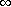, enter -INFINITY or INFINITY.)

f(x) = e^x/1+e^x

find the horizontal and vertical assymptotes?

find the interval whr f is increasing?

Find the inflection point.
( 5, 6)

Find the interval where the function is concave up.
( 7, 8)

Find the interval where the function is concave down.
( 9, 10)

Edited by Miggi - 15 years ago

Quote

Sonia

@Miggi

Inactive

Posted: 15 years ago

#232

Can anyone plz check this?

Consider the function below. (Give your answers correct to two decimal places. If you need to use -

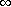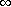, enter -INFINITY or INFINITY.)

f(x) = e^{-1/(x + 9)}

(a) Find the vertical and horizontal asymptotes.
x = 1
y = 2

(b) Find the intervals where the function is increasing.
( -infinity,-9) union

( 9,infinity)

(c) Find the inflection point.
( -8.5, e^-2)(does anyone know wht would be the value of e^-2)

Find the intervals where the function is concave up.
( -infinity,-9) union

( -9,-8.5)

Find the interval where the function is concave down.
( -8.5, infinity)

Edited by Miggi - 15 years ago

Quote

Looks like you are new here. Register for free, learn and contribute.

akhl

@akhl

Dazzler

Posted: 15 years ago

#233

Originally posted by: Miggi

hey thnx a lot i also tried to do this ques but my answer is differnet.

I just have one question

in part a when u found the first derivative to be 8x-4x^3, after factorizing it u get 4x(2-x^2) right? but how did u get 2-x^2 to be x-2 and x+2? i mean shouldn't it be x^2-4 so tht we can write it as x-2 and x+2? i am getting confused about this. hope u can help :) as always:)

You are right. I edited my answers above. Check all the steps again. The part d is about sketching the graph. Can you do that part?

Quote

akhl

@akhl

Dazzler

Posted: 15 years ago

#234

Originally posted by: Miggi

Can anyone plz check this?

Consider the function below. (Give your answers correct to two decimal places. If you need to use - or , enter -INFINITY or INFINITY.)

f(x) = e^{-1/(x + 9)}

(a) Find the vertical and horizontal asymptotes.
x = 1
y = 2

(b) Find the intervals where the function is increasing.
( -infinity,-9) ( 9,infinity)

(c) Find the inflection point.
( -8.5, e^-2)(does anyone know wht would be the value of e^-2)

Find the intervals where the function is concave up.
( -infinity,-9) ( -9,-8.5)

Find the interval where the function is concave down.
( -8.5, infinity)

f(x) = e^-1/(x+9)

lim f(x) = e^-infinity = 0

x-> -9+

lim f(x) = e^-(-infinity) = e^infinity = infinity -------------(1)

x-> -9-

From equation (1), x = -9 is vertical asymptote

lim f(x) = e^-1/infinity = e^-0 = 1

x-> infinity

Therefore y = 1 is horizontal asymptote

f ' (x) = e^-1/(x+9) * 1/(x+9)^2 -------------------------(2)

f ' (x) is not defined at x = -9 and it is positive at all other values of x

Therefore f(x) is increasing in

( -INFINITY,-9) (-9,INFINITY)

Note that both parts of the interval have -9. Your other answers are correct.

e^-2 to 2 decimal places is 0.14

Check the steps.

Quote

Sonia

@Miggi

Inactive

Posted: 15 years ago

#235

hey thnx :) could u please help in other questions too?

Quote

Sonia

@Miggi

Inactive

Posted: 15 years ago

#236

Consider the function below. (If you need to use -

, enter -INFINITY or INFINITY.)

f(x)=sqrt(x^2+6) -x

(a) Find the horizontal asymptote.
y = 0

(b) Find the interval where the function is decreasing.
-infinity , infinity

(c) Find the interval where the function is concave up.
-infinity , infinity

could you plz check this one too?

Edited by Miggi - 15 years ago

Quote

akhl

@akhl

Dazzler

Posted: 15 years ago

#237

Originally posted by: Miggi
Consider the function below. (If you need to use - or , enter -INFINITY or INFINITY.)
f(x)=sqrt(x^2+6) -x

(a) Find the horizontal asymptote.
y = 0

(b) Find the interval where the function is decreasing.
-infinity , infinity

(c) Find the interval where the function is concave up.
-infinity , infinity

could you plz check this one too?

Good. All answers are correct. Make sure to use interval notation ( ) as

(-INFINITY, INFINITY)

Quote

akhl

@akhl

Dazzler

Posted: 15 years ago

#238

Originally posted by: Miggi

Consider the function below. (Round the answers to two decimal places. If you need to use - or , enter -INFINITY or INFINITY.)

f(x) = 2x tan(x)
-p/2 < x < p/2

(a) Find the interval where the function is increasing.
( 1, 2)

Find the interval where the function is decreasing.
( 3, 4)

(b) Find the local minimum value.
5

(c) Find the interval where the function is concave up.
( 6, 7)

f(x) = 2 x tanx---------------------------------(1)

f ' (x) = 2 x sec^2 x + 2 tanx

f ' (x) = 2(x sec^2 x + tanx) ---------------(2)

f ' (x) = 0 at

x sec^2 x + tan x = 0

x sec^2 x = -tanx

x/cos^2 x = -sinx/cosx

x = -sinx cosx

x = -1/2 * 2 sinx cosx

x = -1/2 * sin(2x)

sin(2x) = -2x

This is true only at x = 0 but f ' ( x ) is not defined at this point.

f ' (x) is continuous at all points at which f (x) is defined.Therefore, in any interval which does not contain x = 0, f ' (x) should have the same sign everywhere as changing sign would mean that f ' (x) is 0 somewhere, which has been shown to be not possible.

Consider a point x = -pi/4 in the interval -pi/2 < x < 0

f ' (x) = 2 [(-pi/4) * sec^2(-pi/4) + tan(-pi/4)]

On calculating we get f ' (x) < 0

Therefore f (x) is decreasing in -pi/2 < x < 0

In the interval 0 < x < pi/2,

x > 0, sec^2 x > 0 and tan x > 0

Therefore f ' (x) = 2(x sec^2 x + tanx) > 0

Therefore f(x) is increasing in 0 < x < pi/2

Find the interval where the function is increasing.
(0, pi/2)

Find the interval where the function is decreasing.
(-pi/2, 0)

b) x = 0 is the only point at which f ' (x) changes sign from negative to positive. Therefore there is local minimum at x = 0

f( 0 ) = 2 * 0 * tan0 = 0

(b) Find the local minimum value.
0

c) From equation (2),

f ' (x) = 2(x sec^2 x + tanx)

f '' (x) = 2(x * 2secx * secx * tanx + sec^2 x + sec^2 x)

f '' (x) = 2(2 * x sec^2 x * tanx + 2 * sec^2 x)

f '' (x) = 4 sec^ x (x tanx + 1)

For concave up, f '' (x) > 0

4 sec^ x (x tanx + 1) > 0

xtanx + 1 > 0 (as 4 sec^2 x cannot be negative anywhere)

x tanx > - 1

In both -pi/2 < x < 0 and 0 < x < pi/2, both x and tanx are of same sign.

Therefore x tanx > 0

Therefore x tanx > -1

Thus the condition for concave up is satisfied.

(c) Find the interval where the function is concave up.

(-pi/2, 0) U (0, pi/2)

Quote

Sonia

@Miggi

Inactive

Posted: 15 years ago

#239

Find the inflection points in f(x)= ln(x^4+27) i found 3 and 4.44 and -3 and -4.44 but the website says its wrong i am confused :(?

plus what are the inflection points in e^x/1+e^x i found 0 but not sure what the second 1 is ?

Quote

akhl

@akhl

Dazzler

Posted: 15 years ago

#240

Originally posted by: Miggi

Find the inflection points in f(x)= ln(x^4+27) i found 3 and 4.44 and -3 and -4.44 but the website says its wrong i am confused :(?[/quote]

f ' (x) = 4x^3/(x^4 + 27)

f '' (x) =[( x^4+27) * 12x^2 - 4x^3 * 4x^3]/(x^4+27)^2

f '' (x) =[( x^4+27) * 12x^2 - 16x^6]/(x^4+27)^2

For inflction points

f '' (x) =0

(x^4+27)*12x^2 = 16 x^6

Dividing by 4x^2

(x^4+27)*3 = 4x4

3x^4 + 81 = 4x^4

x^4 = 81

x = -3, 3

Ans: -3, 3

How did you get 4.44 and -4.44 ?[/quote]

[quote]

plus what are the inflection points in e^x/1+e^x i found 0 but not sure what the second 1 is ?